How would you design an efficient, macro-economic simulation of an irregular series of capacity upgrade steps deployed separately at each base-station site in a mobile network where the local growth in demand (and timing of required upgrades) varies by site?
 We unveiled a readily parameterised STEM model at the recent STEM User Group Meeting
which makes a realistic and justifiable simulation of the actual requirement without
having to ‘hire a graphics card’ to do all the processing or an ‘army
of helpers’ to gather countless inputs per site.
We unveiled a readily parameterised STEM model at the recent STEM User Group Meeting
which makes a realistic and justifiable simulation of the actual requirement without
having to ‘hire a graphics card’ to do all the processing or an ‘army
of helpers’ to gather countless inputs per site.
The modelling context
Planning for the evolution of a mobile network must anticipate the transition from coverage constraint to bandwidth constraint. This usually involves an initial roll-out of a certain base capacity – typically varying by geo-type classifications of subscriber density – and then a sequence of progressive upgrades, through:
- incremental capacity (extra channel elements, carriers, etc.), and then
- software upgrades to boost the underlying transmission efficiency when the available spectrum resources are exhausted.
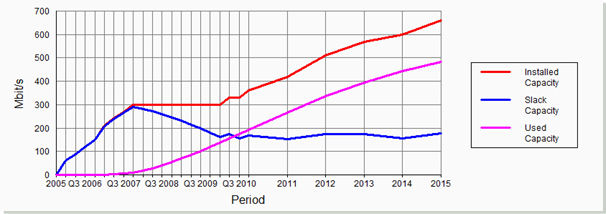
Figure 1: Transition from coverage constraint to bandwidth constraint
The complexity
First of all, the upgrade steps are far from linear:
- you can only add so many channel elements before the next carrier is required
- at some point, the progression switches from hardware additions to software upgrades
- each of these steps offers a different bandwidth or efficiency dividend.
Modelling these steps alone would not be such a challenge, but then the second compounding factor is the variation in timing at individual sites, even within a given density classification.
The actual timing of required upgrades at any individual site depends on the local patterns of demand at that site:
- these will inevitably vary around the average evolution which one might infer from the network average
- these variations increase the geographical overhead of slack capacity and bring forward the timing of each upgrade at the ‘hottest site’.
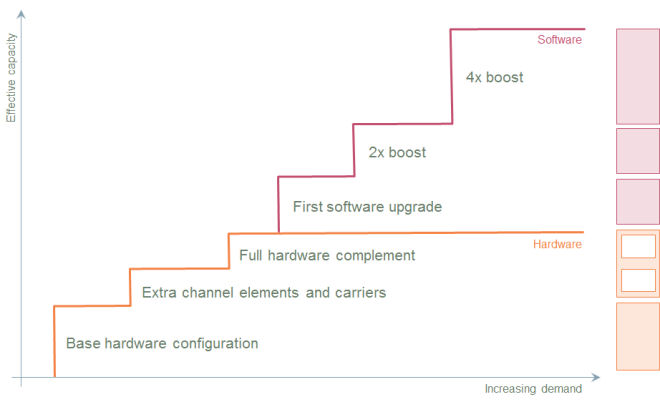
Figure 2: Typical upgrade profile at an individual site (Assume individual sectors of a tri-sector configuration are upgraded together, or treat as discrete sites)
What we wish to simulate in a lean way is the kind of superposition illustrated below!
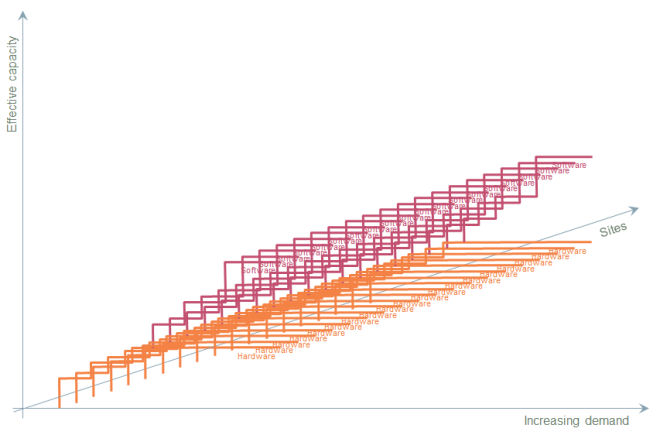
Figure 3: Aggregation of upgrades across discrete sites
The central issue
If you want to build a model which might be intended:
- to project the revenue / cost returns of possible roll-out scenarios, or
- to compare the economic performance of different vendor solutions (where the detailed configuration may even imply a different site map)
Then it is not practical in any useful time-frame (and hence not desirable either) to attempt to simulate down to the individual site, especially if there is a credible alternative.
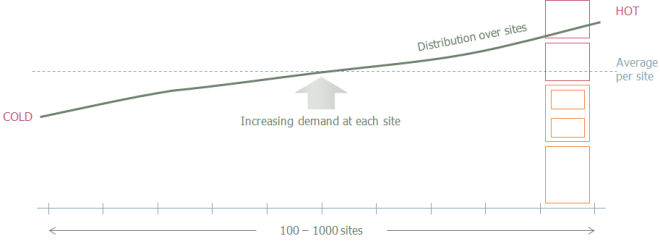
Figure 4: The shape of the problem
Two years ago we presented a very detailed simulation chain which:
- first partitions the demand between initial coverage and progressive upgrade steps, and then
- skews the take-up to allow for one upgrade step kicking off at the ‘hotter sites’ while an earlier step continues elsewhere
However, a chance question in a training situation six months ago has prompted a quite different and rather more holistic approach based on an outright prediction of when each progressive step should commence:
- the outputs are certainly more realistic, in terms of potentially greater temporal overlap of multiple upgrade stages
- the numbers are perhaps easier to justify – for you to judge presently!
- the model structure is far simpler, and consequently more robust
- (from experience, the original approach almost defied explanation!)
We outline and compare these two approaches in turn. For more details of the specific
modelling techniques employed, please register to
download a copy of the STEM User Group Meeting 2011 proceedings.
Previous solution: a partitioned upgrade chain
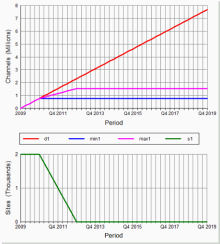
The original demand is partitioned between that which can be satisfied with the original R99 configuration, and ‘the rest’.
This remainder is partitioned again between that which can be satisfied by the first upgrade step, and ‘the rest’.
This process is repeated for each upgrade step.
An additional refinement is made to ‘split the demand’ to bring forward the first installation of step n before step n – 1 is quite finished, though this proves to be rather less effective than first thought.
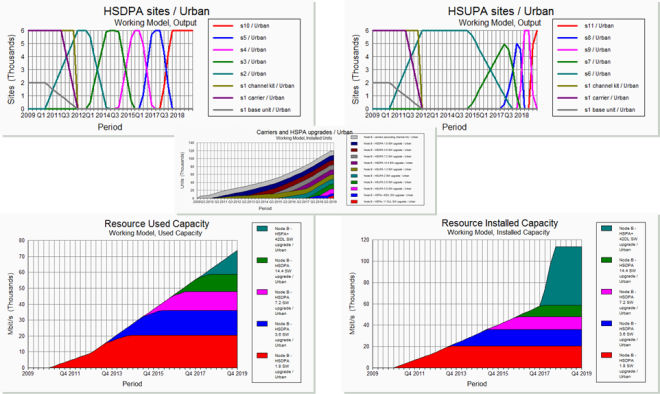
Figure 5: Results showing overlapping upgrade steps
New solution: absolute timing of upgrade limits
For each upgrade step in turn, we consider a single hypothetical resource with capacity equivalent to all of the steps up to and including this upgrade.
Using a Monte Carlo deployment model, STEM estimates how soon more than one unit per site is required.
We infer that the first unit of upgrade n is required when step n – 1 reaches this threshold, up to its own threshold when every site has received this upgrade step.
The result is a more holistic spread of upgrades such that three or more parallel upgrade steps may be rolled out at different sites in the same year.
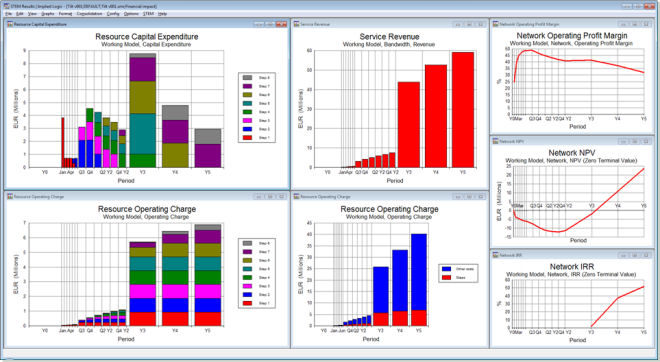
Figure 6: Capex by upgrade step and related financial results
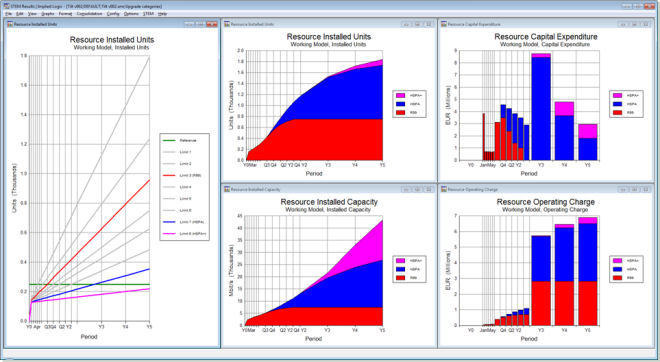
Figure 7: Reporting by category: R99 / HSPA / HSPA+
So: which solution is better?
|
Partitioned upgrade chain |
Absolute timing prediction
|
| Scientific/auditable | Intuitive |
| Works in bandwidth terms | Works in terms of units |
| Fragile, house of cards | ‘Process independence’ |
| Extensive explanation required | Only one generic concept to grasp |
| Still involves a fudge | Fudge is easy to ‘prove’ / defend |
| Entirely to ‘get right results’ (impossible to calibrate) | Less causal but more likely to be in the right ballpark |
| Very limited overlap of steps | Naturally wider spread of steps |
Figure 8: Pros and cons of the two solutions
It should be noted that the new technique assumes a normal distribution of demand across all sites. If, as is likely in practice, there are significant jumps or bands in the distribution over the whole network, then the results will always be better if each consistent band is analysed separately. Such a partitioning by classifications of subscriber location density is usually referred to as ‘geo-typing’, and is a standard modelling practice.

Figure 9: Illustration of sites partitioned by classifications of subscriber density
However, whether you can distinguish 4 or 16 separate geo-types, there are still likely to be hundreds of sites in each sample.
The benefits of getting a lean model running quickly, combined with the evident ‘correctness’ of the results, may easily override concerns about the apparent ‘hand waving’ aspect of this new methodology. Its compact structure and simple parameterisation make it a much more manageable candidate for replicating across multiple geo-types.
For more details of the specific modelling techniques employed, please register to
download a copy of the STEM User Group Meeting 2011 proceedings.