STEM 7.4 includes a long-awaited refinement to the calculations for geographical
deployment in the case when a resource specifies a Maximum
Utilisation constraint too. We have also introduced a new
Minimum Slack Capacity input which demands a fixed overhead of slack capacity
in addition to the variable overhead for Maximum Utilisation.
This article is an extract from the new documentation for STEM 7.4 and describes
the interaction of these two overheads with the existing calculations for geographical
deployment, complete with relevant examples.
1. New models will Deploy With Utilisation
When the Maximum Utilisation feature (MU) was added
to STEM, it was considered quite separately from Deployment,
so that:
- the MU constraint considers only total demand (ignoring sites)
- the deployment calculation allows for the notional utilisation of resources at each
site to vary from 0 to 100% (rather than the lower percentage which may be envisaged
by the Maximum Utilisation input).
This behaviour was unintuitive at best and so STEM 7.4 now limits the range of notional
utilisation at each site to 0–MU if the new input Deploy With
Utilisation = Yes (which is the new default
behaviour). Utilisation at the ‘hottest’ site will not exceed MU, and will be proportionately lower at other sites (as shown in the two figures below), resulting in lower overall utilisation than without the MU constraint.
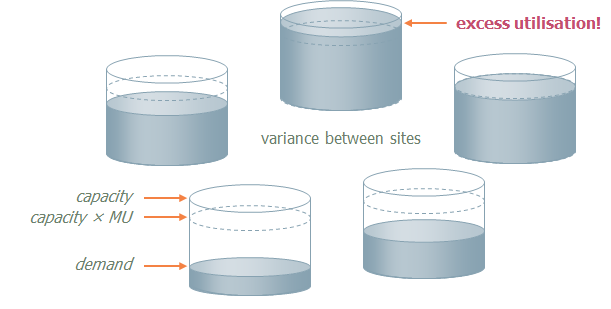
Figure 1: Illustration of original interpretation with Deploy
With Utilisation = No
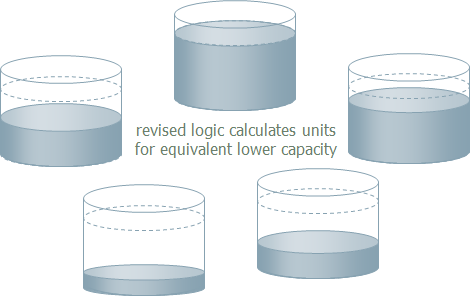
Figure 2: Illustration of refined interpretation with Deploy
With Utilisation = Yes
Thus, a Maximum Utilisation constraint will now
impact the Installed Units result directly. Previously
(or with Deploy With Utilisation =
No
) it would only make a difference if the specified overall Maximum Utilisation
was lower than that which would already result from an existing allowance for deployment.
These new installation results will match those of an unconstrained resource with
equivalent input Capacity =
c . MU (where c is the
Capacity of the original resource), whereas this was not so before
(or with Deploy With Utilisation =
No).
Legacy behaviour
STEM 7.4 will set the input Deploy With Utilisation
= No for all resources when loading an older model in
order to maintain the original results. However, you may wish to review those results
(and this setting going forward) if any resources in your model do combine the Maximum Utilisation and Deployment
features.
Example
Consider a resource with the following input characteristics and for which the overall
demand gradually increases from zero to 1000 subscribers over ten years:
- Capacity = 50 Ports
- Maximum Utilisation = 80%
- Sites = 10
- Distribution = Monte Carlo.
Figure 3 below compares the original (STEM 7.3) results for
two scenario variants, Lean and
Variable, which switch the Maximum Utilisation
input between 100% and 80%.
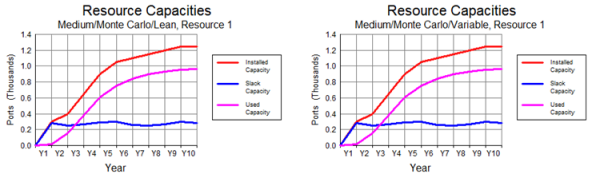
Figure 3: No difference with Maximum Utilisation
when Deploy With Utilisation = No
The chart on the right (where Maximum Utilisation
= 80%) looks exactly the same! Indeed, there is no difference
at all, because the Deployment calculation already
results in sufficient slack capacity for the Utilisation Ratio
result never to exceed 78%.
Figure 4 below shows the results for a third scenario
variant, Variable NEW, which in contrast sets the
new input Deploy With Utilisation =
Yes.
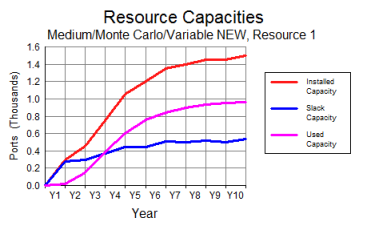
Figure 4: Increased overhead with Maximum Utilisation
when Deploy With Utilisation = Yes
You can see that a greater overhead of slack capacity is installed; in addition
to the more or less fixed geographical overhead (roughly 250 ports), now there
is also a variable component (in proportion to the demand) which amounts to another
250 ports by the end of the model (equivalent to the 25% of demand required
to ensure that utilisation would not exceed 80% at any one site). The combined effect
results in an overall utilisation which never exceeds 66% within the model run.
(You may find it instructive to consider how the installed units would compare
for a resource with inputs Capacity =
40 Ports and Maximum Utilisation
= 100%; i.e., the same effective capacity of the original resource.)
2. Fixed and variable overhead capacity
The Maximum Utilisation input tells STEM to install
an additional variable amount of slack capacity (usually
bandwidth) in proportion to the nominal total demand to allow for transient peaks
in usage. Other situations call for a fixed overhead
of spare capacity (typically ports) which might be reserved as immediately available
spare capacity in the event of card failure or to enable rapid provisioning for
new customers.
This fixed overhead for a resource can now be specified explicitly with a new Minimum Slack Capacity input (MSC), found in the
Capacity and Lifetime dialog:
- in the simpler case where there is no geographical Deployment
to consider, STEM adds this MSC to any non-zero required demand before rounding
up to determine how many units must be installed, thereby ensuring that there will
always be the slack capacity required for as long as there is any current demand
- the MSC input is ignored if there is no current demand for a given resource
- the MSC input is not limited to the unit Capacity
of a resource, so it can lead to multiple, wholly slack units being installed if
so required.
For a resource with inputs Capacity =
50 and Minimum Slack Capacity =
15, the effect is just that the next unit will be installed when
the demand exceeds 35, 85, 135, etc., rather than the usual 50, 100, 150 and so
on.
Minimum Slack Capacity and
Deployment
STEM will allow for the same fixed overhead at each site if the new input
Deploy With Utilisation = Yes. Otherwise it
is only applied as a single overhead on the overall demand.
Figure 5 below compares the results for two scenario
variants, Lean and Fixed
NEW, which switch the Minimum Slack Capacity
between 0 and 15 ports, respectively, in a situation where the overall demand gradually increases
from zero to 1000 subscribers over ten years (with a Monte
Carlo distribution over 10 sites).
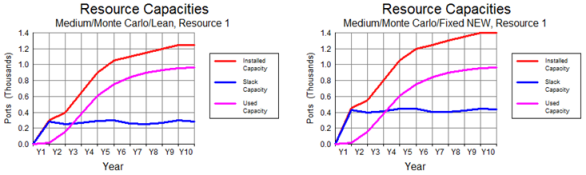
Figure 5: Additional fixed overhead with Minimum Slack Capacity
when Deploy With Utilisation = Yes
The deployment calculation allows for the notional slack capacity at each site to
vary in the range 15–65 ports (average of 80% of a unit) rather than the unconstrained
0–50 ports (average of 50%), resulting in an extra 10 × 30% slack capacity
(equivalent to three more units; i.e., the 150 subscriber difference you can see
on the chart).
Minimum Slack Capacity and
Maximum Utilisation
The variable overhead required by a Maximum Utilisation
constraint makes most sense for a continuously variable demand like bandwidth where
some operational headroom is often left to allow for temporal fluctuations in demand.
In contrast, the fixed overhead of Minimum Slack Capacity
is more likely to be used for a discrete capability such as ports where it is common
to leave some capacity free for immediately available spares, or to minimise delay
when adding new customers. Therefore, it is unlikely in practice that the two effects
will be required for the same resource.
However, it is not an error to specify both inputs in parallel and the resulting
calculation is additive: STEM installs sufficient
capacity to allow for the specified minimum slack in addition to the variable overhead
on top of the basic demand. In the single site case, the capacity installed for
a demand, d, will be at least
d/MU + MSC.
STEM does not apply the maximum utilisation overhead to the minimum
slack part as this is not required if the minimum slack represents spares
which are available to swap with other used parts.
Alternatively, if the minimum slack is capacity reserved for adding new customers,
then an inflated capacity would have to be reserved to allow for the usual maximum
utilisation to hold if/when those customers are added. Therefore, if
CB is the intended customer buffer, then you should consider setting
the input Minimum Slack Capacity =
CB/MU. The resulting capacity installed
at a single site will be at least d/MU
+ CB/MU = (d + CB)/MU.
For a resource with inputs
Capacity = 50,
Maximum Utilisation = 80% and
Minimum Slack Capacity = 15,
the combined effect is that the next unit will be installed when the demand exceeds 28 (= 35
× 0.8), 68, 108, etc., rather than the usual 50, 100, 150. This allows for at least
15 spares, or the potential to add 12 (= 15 × 0.8) customers without having to install
an extra unit.